💡 Challenges
Enc-and-MAC
In the first challenge, we will consider the Enc-and-MAC construction. The assumptions on the cryptographic primitives are the same as in the chapter First Proof: The symmetric encryption is IND-CPA-secure and the MAC is SUF-CMA-secure.
Try to prove that Enc-and-MAC is IND-CPA-secure using CryptoVerif. As you may already know, that cannot be proven as attacks exist.
In this challenge, you should inspect CryptoVerif’s output and understand why the sequence of games failed.
Note that CryptoVerif cannot find attacks. However, you should use CryptoVerif’s output to derive a concrete attack on the Enc-and-MAC construction.
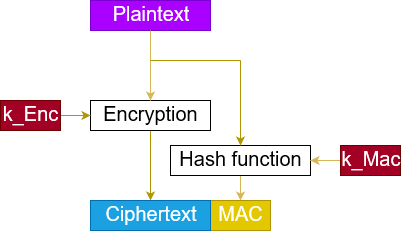
The Enc-and-MAC construction works as follows.
- Encrypt the plaintext, resulting in a ciphertext.
- Compute the MAC over the plaintext.
- Concatenate the ciphertext and this MAC.
You can see a visualization of this construction on the right-hand side.
❓ Don’t know how to proceed? Click here.
The input file is almost the same as enc-then-MAC-IND-CPA.ocv discussed in the chapter First Proof.
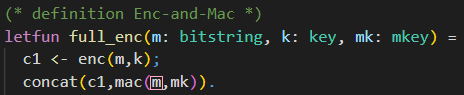
For this task, you need to rewrite the definition of full_enc to match Enc-and-MAC instead of Enc-then-MAC.
Show solution
Solution: Definition Enc-and-MAC
To rewrite the definition of the Enc-then-MAC encryption to the Enc-and-MAC encryption, you need to change what the MAC will be computed over. For Enc-and-MAC, we compute the MAC over the plaintext m.
Explanation: How the proof fails
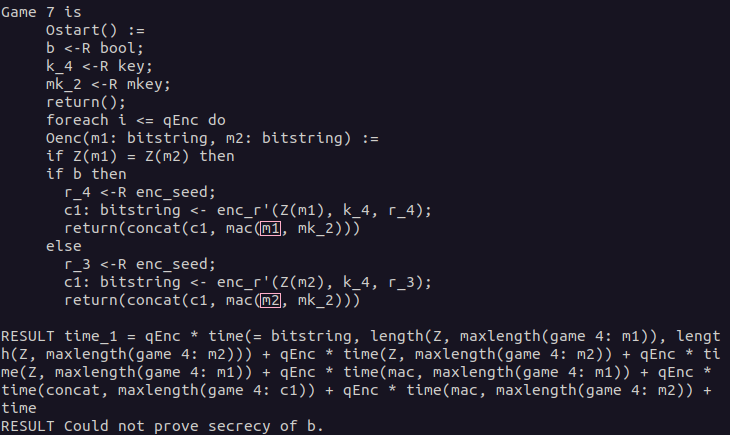
In the IND-CPA proof for Enc-then-MAC presented in the chapter First Proof, we saw that CryptoVerif was able to merge the branches depending on the value of b. This was possible as the expressions were semantically the same in both branches.
For the Enc-and-MAC construction, this is not possible. When you have a look at the highlighted parts in the CryptoVerif output below, you will see that in the upper branch, the MAC is computed over the plaintext m1 and in the lower branch over the plaintext m2. This prevents merging those branches. At this point, CryptoVerif does not find another way to prove the secrecy of b.Solution: Derive attack on Enc-and-MAC
Now we want to use the output of the failed CryptoVerif proof to derive an attack against the Enc-and-MAC construction. As shown before, the proof failed because the branches of the if statement could not be merged. This was because the MACs were computed over the different plaintexts m1 and m2. When we try to derive an attack against the Enc-and-MAC construction, we will start at this part.Our goal is to show that the Enc-and-MAC construction is not necessarily IND-CPA-secure when the encryption scheme is assumed to be IND-CPA-secure and the MAC is considered SUF-CMA-secure. We know that the fact that the MAC is computed over the plaintext instead of the ciphertext is probably connected to the reason why the proof fails.
As we want to derive an attack against the IND-CPA security, we aim for revealing any information about the plaintext. The most simple way of doing so is by revealing the whole plaintext. Combine this with the fact that SUF-CMA security of a MAC does not make any statements about confidentiality. You can define a MAC named MAC using a SUF-CMA secure MAC named MAC' as follows.
It is easy to prove that the newly constructed MAC is still SUF-CMA-secure. For further information, you can have a look at Krawczyk's work (Chapter 4). Instantiating the Enc-and-MAC construction with the newly constructed MAC, it is quite obvious that it cannot be IND-CPA-secure. The message encrypted is always appended to the MAC and is directly revealed in the Enc-and-MAC ciphertext. This way, the adversary can say which plaintext has been encrypted with probability 1.
💡 Feel free to experiment with CryptoVerif if you want to. For example, you can use CryptoVerif to prove that the newly constructed MAC revealing the message is still SUF-CMA-secure.
Enc-then-MAC IND-CCA2
In the second challenge, we will consider the
Enc-then-MAC
construction again. The assumptions on the cryptographic primitives are the same as in the chapter First Proof: The symmetric encryption is IND-CPA-secure and the MAC is SUF-CMA-secure.
Your goal is to prove that Enc-then-MAC is then
IND-CCA2-secure using CryptoVerif.
You can orientate yourself on the input file enc-then-MAC-IND-CPA.ocv presented in the chapter First Proof. You may require to have a look at hints 4 and 5 as they contain CryptoVerif syntax not captured in this tutorial beforehand.
❓ Need any hints? Click here.
💡 Hint 1
Consider the differences between the IND-CPA game and the IND-CCA2 game. What is new?
💡 Hint 2
The IND-CCA2 game requires a decryption oracle.
Did you tell CryptoVerif how the Enc-then-MAC decryption looks like?Solution: Decryption Enc-then-MAC
💡 Hint 3
The IND-CCA2 game requires a decryption oracle.
Did you add the decryption oracle? You can orientate yourself on the encryption oracle presented in the chapter First Proof.
Note that you should not implement the decryption oracle as a left-or-right oracle.💡 Hint 4
Did you remember to exclude how any adversary can trivially win the IND-CCA2 game?
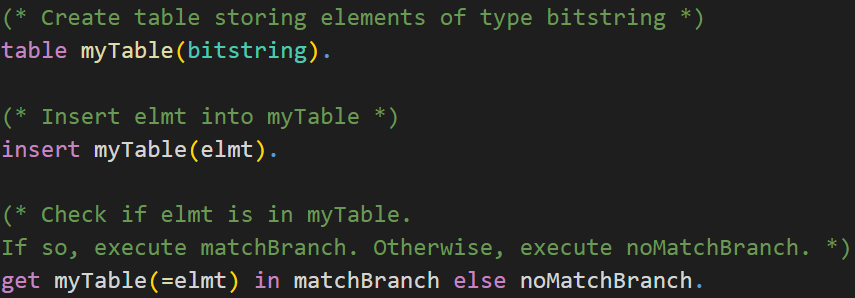
You may use tables in CryptoVerif to do so. Check the syntax of tables in CryptoVerif below.CryptoVerif Syntax: Tables
💡 Hint 5
In the IND-CCA2 game, the adversary can access the encryption oracle and the decryption oracle. The adversary can choose the order he makes requests to the oracles, but in CryptoVerif only one oracle can be called at a time.
Check the syntax of parallel composition of oracles in CryptoVerif below.CryptoVerif Syntax: Parallel composition of oracles
Show solution
Solution: Decryption Enc-then-MAC
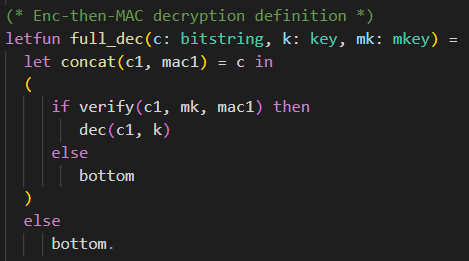
The Enc-then-MAC decryption function full_dec has three parameters. It requires the ciphertext c of type bitstring, the encryption key k of type key, and the MAC key mk of type mkey.
First, it separates the ciphertext c of the Enc-then-MAC encryption back into the actual encryption ciphertext c1 and the MAC mac1. If the ciphertext c was of incorrect format and therefore could not be split into c1 and mac1, the function returns bottom.
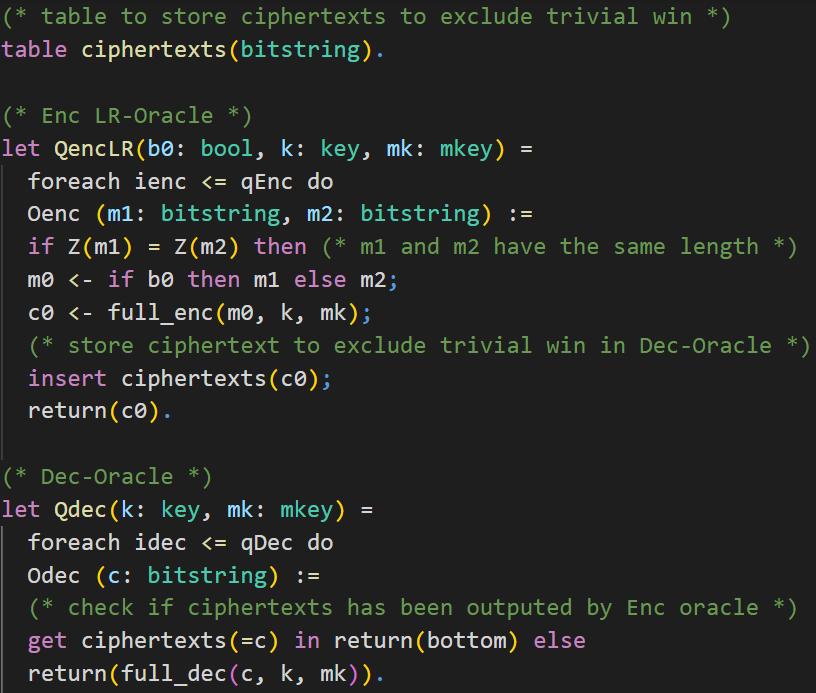
Then, it is checked whether the MAC mac1 is valid. This is done by calling the verification function verify, providing the ciphertext c1, the MAC key mk, and the MAC mac1 as parameters. If the verification succeeds, the decryption of the ciphertext c1 under the decryption key (same as the encryption key) k is returned. If the verification fails, the function returns bottom.Solution: Enc and Dec oracle (exclude trivial win)
The encryption oracle QencLR is almost the same as in the IND-CPA proof presented in the chapter First Proof. As we need to give an adversary access to a decryption oracle, we require preventing that an adversary can win the IND-CCA2 game trivially. That is, excluding that an adversary can send a ciphertext produced by the encryption oracle directly to the decryption oracle.
We do this by keeping track of the returned ciphertexts in a table. First, we create a table called ciphertexts, which can contain elements of the type bitstring. Inside the oracle Oenc we will insert the generated ciphertext c0 into the table.The decryption oracle Qdec has two parameters. It requires the encryption key k of type key and the MAC key mk of type mkey. Similar to the encryption oracle, we use oracle replication for the decryption oracle as well. The oracle Odec takes a ciphertext c as input. Note that the decryption oracle is not a left-or-right oracle, so we do not have inputs like c1 and c2. We check whether the ciphertext c, queried by the adversary, is inside the table ciphertexts and has therefore been returned by the encryption oracle earlier. If this is the case, the function returns bottom. Otherwise, the Enc-then-MAC decryption is returned.
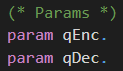
The parameters qEnc and qDec used for the oracle replication are declared at the top of the input file.
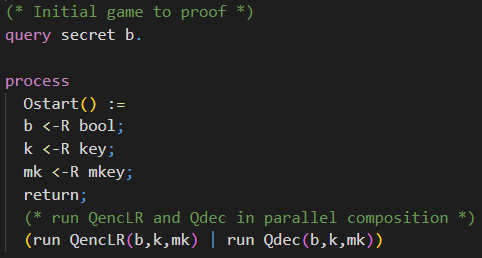
Solution: Initial Game
The initial game is almost the same as the initial game for the IND-CPA game presented in the chapter First Proof. The only difference is that the adversary has access to a decryption oracle additionally. We achieve this by running both oracles in parallel composition (check Hint 5).
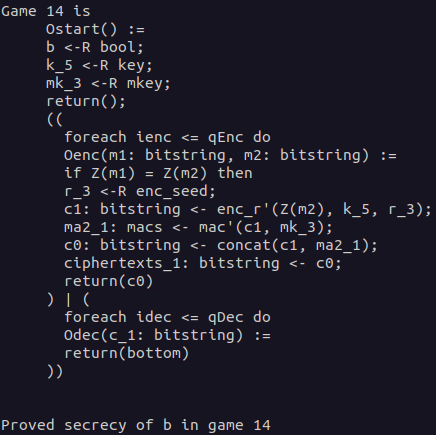
Take a look at the last game and convince yourself that the secrecy of b can be proven in Game 14.
Show last game