📚 First Proof

In this chapter, we will have a look at a first proof using CryptoVerif. You will be guided to gather an understanding of how to work with CryptoVerif.

We will consider the Enc-then-MAC construction. Our goal is to show that Enc-then-MAC is IND-CPA-secure, assuming the symmetric encryption is IND-CPA-secure and the MAC is SUF-CMA-secure.

Enc-then-MAC

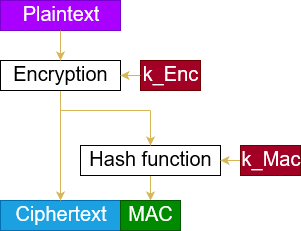
The Enc-then-MAC construction works as follows.

1. Encrypt the plaintext, resulting in a ciphertext.
2. Compute the MAC over this ciphertext.
3. Concatenate the ciphertext and this MAC.

You can see a visualization of this construction on the right-hand side.

Input file

In this section, we will build the input file for the proof together. CryptoVerif takes this file and tries to prove the queries we defined using the sequence of games technique.

ℹ️ Note that we will not strictly walk through every line of code from top to bottom. We will skip some lines for didactic reasons and explain them at the appropriate places.

Cryptographic assumptions

We start with the cryptographic assumptions we make for the cryptographic primitives used. In our case, this is that the symmetric encryption is IND-CPA-secure and the MAC is SUF-CMA-secure.

CryptoVerif provides a library containing many cryptographic assumptions you can use (see docs/manual.pdf, Chapter 6). It is also possible to create your own assumptions.

You can see the code snippets for telling CryptoVerif that enc is IND-CPA-secure and mac is SUF-CMA-secure in the following.

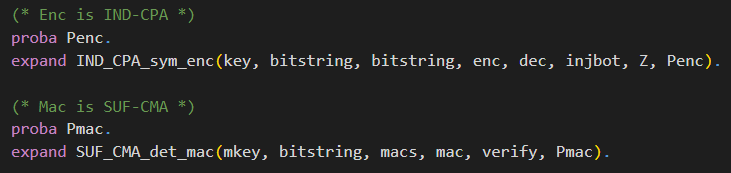
The macros IND_CPA_sym_enc and SUF_CMA_det_mac defined in default library default.ocvl are expanded. For a better understanding, we will discuss the technical side with the example of the IND_CPA_sym_enc macro.

First, let us inspect the meaning of the parameters of this macro:

1. type of keys,
2. type of plaintexts,
3. type of ciphertexts,
4. encryption function,
5. decryption function,
6. function to inject the type bitstring into the type bitstringbot. The decryption returns either a bitstring (plaintext) or bottom (when the decryption fails). The type bitstringbot contains all bitstrings and bottom. bitstringbot is the return type of the decryption function.
7. function from bitstring to bitstring, modeling the leakage of the encryption. We usually interpret this as the leakage of the length of the plaintext.
8. probability of breaking the IND-CPA property

The functions enc, dec, injbot and Z are declared by the macro. It is important that they are not declared anywhere else. They can only be used after the macro has been expanded.

The types of keys, plaintexts, ciphertexts, and the probability Penc must be declared before expanding the macro.
As you can see in the code snippet, the probability Penc is declared right before expanding the macro.
The types of plaintexts and ciphertexts are bitstring, a predefined type.
The type of keys is declared at the top of the input file, depicted in the following code snippet. There are also the type declarations for parameters for the macro SUF_CMA_det_mac.

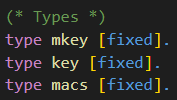
The types are annotated with the label [fixed] meaning that, for example, an encryption key is a bitstring of fixed length. Note that CryptoVerif does not need to know the specific length. Similar as it does not need to know the specific implementation of the symmetric encryption scheme or the MAC.
Note that it is possible to make an exact specification of the length to CryptoVerif.

Now we want to gain a better understanding of how CryptoVerif is doing game transformations. Once again, we will take the IND-CPA assumption as an example.
Let’s have a look at a code snippet from the macro IND_CPA_sym_enc in the default library default.ocvl depicted below.

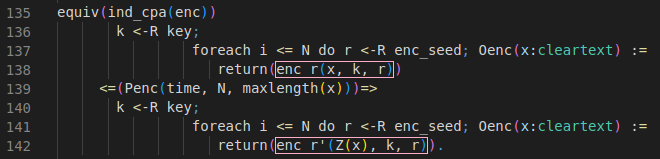
This equivalence defines how the IND-CPA game hop looks like. CryptoVerif will look for code segments matching with the upper block (lines 136-138) and will replace them with the lower block (lines 140-142) to perform this game hop. If it does so, the probability stated in line 139 will be added to the bound of the adversary advantage.

Let’s compare the upper block (lines 136-138) with the lower block (lines 140-142) to see why this equivalence is suitable for the IND-CPA assumption.
We start with a uniformly random sampled encryption key k (line 136+140). The lines 137-138 and lines 141-142 are representing the encryption oracle using replication of the oracle Oenc. Oracles are defined by the usage of ":=".

ℹ️ Replication of oracles are used to indicate that an oracle can be executed multiple times. In the code snippet above, the oracle Oenc is replicated N times. The variable N is no concrete value, but a parameter that will appear as such in the adversary advantage.

Both oracles Oenc take a cleartext x as input, but they differ in their output.
In the upper block, the oracle returns the encryption of the cleartext x under the key k and the encryption seed r (line 138). This matches a regular encryption of cleartexts.
In the lower block, the oracle does not encrypt the cleartext x but the leakage of the encryption Z(x) (line 142). For simplicity, we will interpret the leakage of the encryption as the leakage of the lenght of the cleartext. We assume that Z(x) will return a bitstring with the same lenght as x consisting only of zeros.
This transformation matches the IND-CPA assumption quite well, as the ciphertexts cannot be used to gather any additional information about the cleartexts.

❗️ It is important that the requirements stated by this equivalence are strictly matched to perform this transformation.
If we assume that inside a game the encryption seed r is chosen randomly outside the replication and is reused for each encryption, then CryptoVerif is not allowed to perform this transformation, as the requirements including the correct distribution for each variable are not matched.

Definition Enc-then-MAC

Further, we need to define how Enc-then-MAC works.

For the definition of the Enc-then-MAC construction, we will need a function for concatenation. We are not interested in the concrete implementation of this function.
Therefore, we only declare the function using the keyword fun.
The keyword letfun is used when defining a function, i.e., giving a concrete implementation. We will use this one for the definition of the Enc-then-MAC encryption.

The declaration of the concatenation function is shown in the following.

The function concat takes parameters of type bitstring and macs, and returns a variable of type bitstring. The annotation [data] indicates that this function is injective and its inverse can be computed efficiently.

Now that we talked about the concatenation function, we have everything we need to move on to the Enc-then-MAC construction. The definition of the Enc-then-MAC encryption is depicted in the following.

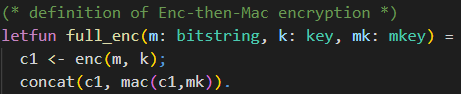
As we want to define the exact behaviour for the Enc-then-MAC encryption, we use letfun for the definition of the function full_enc.

The function has three parameters that are needed.
First, there is the plaintext m of type bitstring. In this model, we consider plain- and ciphertexts as bitstrings. This means we consider cryptographic primitives (e.g., encryption) as mappings from bitstrings to bitstrings.
Further, there are the encryption key k of type key, and the MAC key mk of type mkey.

We will use the encryption function enc declared inside the macro IND_CPA_sym_enc to compute the encryption of the plaintext m under the encryption key k. This ciphertext is then stored in variable c1.
Next, we concatenate the ciphertext c1 with the MAC of the ciphertext c1 under the MAC key mk. This concatenation is the result of our Enc-then-MAC encryption function full_enc.

Note the difference between the usage of “;” and “.” in CryptoVerif.
Sequential execution is denoted by “;”. In the above code snippet, you can see this in the line where c1 is set to the ciphertext. The semicolon indicates that there is a line of code following, which should be executed afterwards.
The line with the concationation is the last expression belonging to full_enc. This block of code is ended with “.”.

Initial game to prove (including oracles)

Now we want to construct the initial game CryptoVerif should try to prove using the sequence of games. In our example, this is the IND-CPA game. Note that for many games, there are oracles the adversary has access to. Here, an encryption oracle from the IND-CPA game is required. We will start with this oracle before proceeding with the initial game.

The code of the encryption oracle is depicted below.

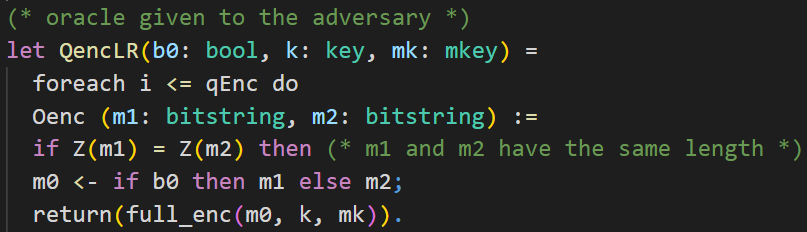
First, let's talk about the keyword let used for this oracle. With this, the subprocess QencLR is defined. The code in this subprocess will be inlined inside the main process we will see later on. It is not required to do it this way. You can also put the whole code inside the main process where you need it. Using this approach, you can structure your code for a lot better readability.

The encryption oracle is implemented as a left-or-right oracle. That means that the oracle receives two plaintexts in each query made by the adversary and always encrypts the left plaintext or always encrypts the right plaintext, depending on the value of the secret bit b0.
Note the relation between IND-CPA security and LoR-CPA security (cf. [ Bellare et al., Theorem 3]).

The oracle Oenc we want to define should be callable by the adversary multiple times. We model this by oracle replication. The oracle can be called qEnc times. qEnc is just a parameter defined at the top of the input file and is not an actual number. The parameter is put into the bound of the adversary advantage at a corresponding game hop.
The adversary can make calls to the oracle. This models the interaction between the adversary and the game.

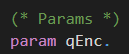
The oracle Oenc takes two plaintexts m1 and m2 as input. As distinguishing ciphertexts of plaintexts with different leakage in the encryption is easy, the oracle should only respond with the ciphertext if the leakage of the received plaintexts is the same.
Remember: Interpreting the leakage of the encryption as the length of the plaintext, this means that m1 and m2 should have the same length. This property is also referred to in many definitions of the IND-CPA assumption.

ℹ️ If-branches cannot be merged in CryptoVerif. This means that expressions that should be executed after the conditioned expression have to be put inside the matchBranch and the noMatchBranch.

The value of m0 is set to m1 or m2, depending on the bit b0. Then, we return the Enc-then-MAC encryption of m0 under the encryption key k and the MAC key mk.
As b0 is fixed for the left-or-right oracle, this means that we always encrypt m1 or always encrypt m2.

In our initial game, we want to prove the secrecy of the bit b. We use the query depicted in the following to tell CryptoVerif what should be proven.

The initial game is displayed in the following code snippet.

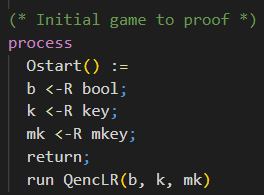
In CryptoVerif the initial game is the main process. This is indicated by the keyword process. There can be only one main process.
Inside this process, we define the oracle OStart. Here you will recognize how this oracle represents the initial game, to be more specific, the IND-CPA game.
The bit b is sampled as a random boolean value, being either 0 or 1. Further, the keys are sampled randomly from their corresponding keyspaces. The encryption key k is uniformly random of type key. The MAC key mk is uniformly random of type mkey.

At this point the initial game is set up, and we want to give control to the adversary. We do this using the keyword return. The adversary can now choose which oracle he wants to call.

With the keyword run, a subprocess is inlined. Therefore, we inline the previously defined subprocess QencLR with the random bit b, the random encryption key k, and the random MAC key mk as parameters. This subprocess contains the encryption oracle that can be called by the adversary against the IND-CPA game.
In the very last line there is no “.” as the file ends here.

Execute

The input file is now ready, and we can execute CryptoVerif to let it try proof our query.
You can find the input file enc-then-MAC-IND-CPA.ocv here.

When in the same directory as the executable cryptoverif you can run CryptoVerif on our created input file using the following command. (The presented input file already exists in the folder examples/basic.)

./cryptoverif examples/basic/enc-then-MAC-IND-CPA.ocv

Output

Let's have a look at the output of CryptoVerif and see how it proved the Enc-then-MAC construction IND-CPA-secure under the given cryptographic assumptions.
CryptoVerif proves the secrecy of bit b in eight games. We will not talk about every game hop. When you take a look at the first game hops, you will see that many game hops are of syntactic nature. Note that the first game is already inlined. Examples for syntactic game hops are expanding if statements or renaming variables.

We will take a closer look at the game hop, where the assumption that the encryption scheme is IND-CPA-secure is used. You can expand the IND-CPA game hop below.

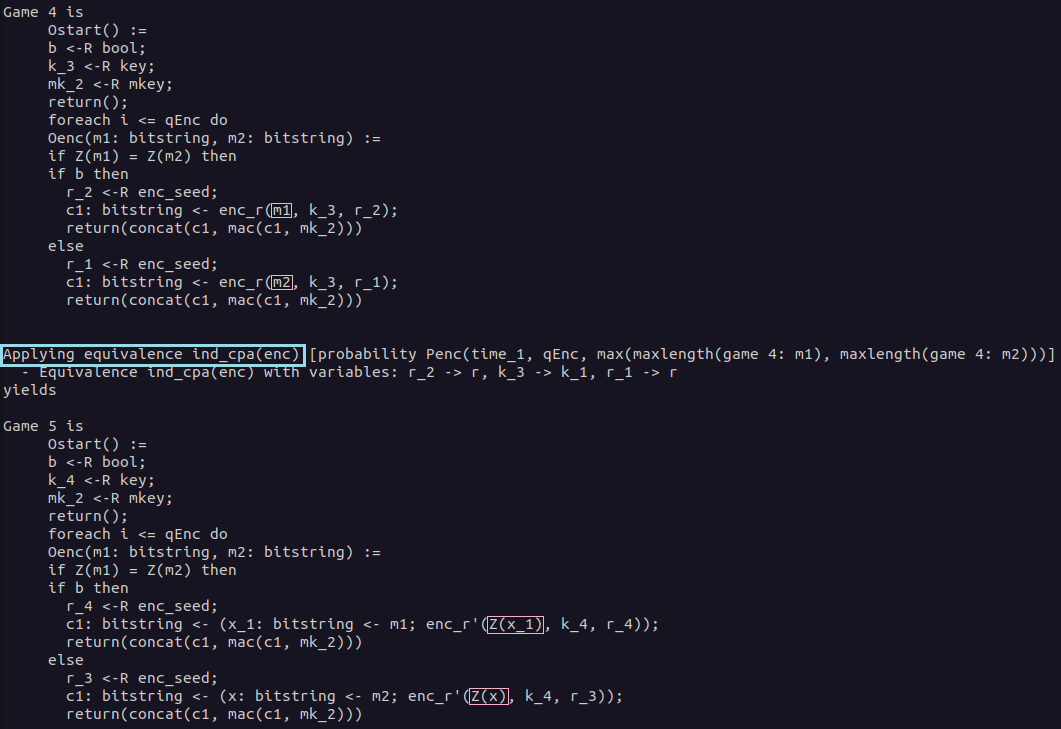
In Game 4, the game before the IND-CPA game hop, you can see that besides some syntactic changes not much has changed compared to the initial game. The previous syntactic game hops are necessary to fulfill the requirements to apply the IND-CPA equivalence. We talked about this equivalence in detail in the section Cryptographic Assumptions.
Depending on the value of bit b either the plaintext m1 or m2 is encrypted using the Enc-then-MAC encryption. For this game hop, we will focus only on the part of the Enc-then-MAC construction where the plaintext m1 or m2 is encrypted using the encryption scheme enc. The plaintexts for this encryption are highlighted in the output of CryptoVerif.
As we told CryptoVerif that the encryption scheme is IND-CPA-secure by expanding the corresponding macro, the defined equivalence can be applied here. As we have previously seen, the plaintext to be encrypted is replaced by the leakage of the encryption of this plaintext. Having a look at the highlighted parts in Game 5, you can see that this equivalence has been applied. Note that the equivalence has been applied twice, once for each branch of the if statement. This equivalence models the IND-CPA assumption.

We will now take a look at the last game hop and understand why the secrecy of bit b can be proven in the last game. You can expand the last game hop (Merging game hop) below.

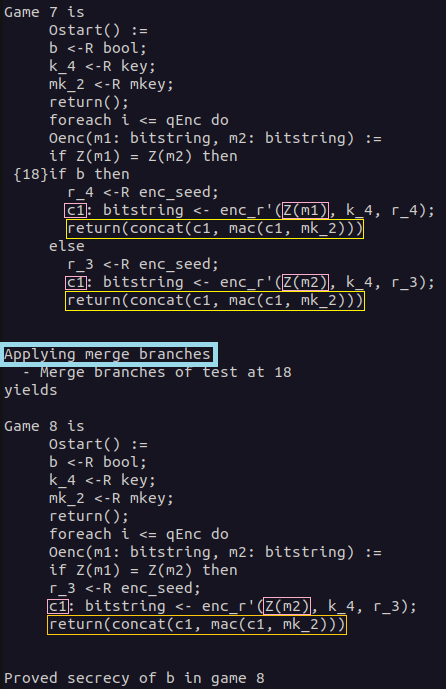
In the last game hop, the branches of the if statement depending on the value of bit b are merged. This is possible as both branches are semantically equal.
First, in both branches, a seed is sampled uniformly at random. The ciphertexts c1 are generated using the same encryption function, the same encryption key, and a uniformly random sampled seed. We have to take a look at the plaintexts that are used for the encryption. In the upper branch Z(m1) is encrypted, while in the lower branch Z(m2) is encrypted. Because of the condition if Z(m1) = Z(m2) then, both values are the same. The return statements are also the same in both branches. Therefore, the branches can be merged.

The bit b was only used in the if statement whose branches we merged with the last game hop. Therefore, it has now become trivial that the secrecy of bit b can be proven, as it is not used anywhere in the game anymore.

In the following, you can see that CryptoVerif proved the secrecy of bit b in game 8. You can also see the bound of the adversary advantage. In the last line, it is stated that all queries have been proven. Therefore, the proof done by CryptoVerif is finished.

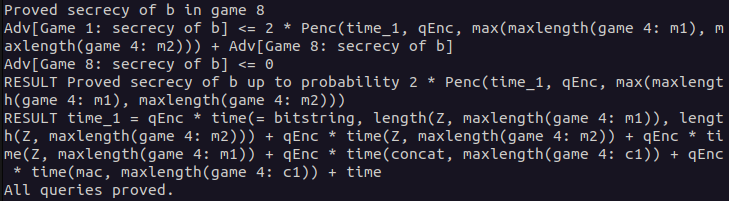
Only the games discussed before in detail are affecting the advantage of the adversary. For simplicity, we will use the term "advantage in game X" when describing the "advantage regarding the secrecy of bit b in game X".
First, you can see that the advantage in game 1 is bounded by twice the probability defined by the IND-CPA equivalence (Penc) plus the advantage in game 8. The factor of two is because the equivalence has been applied twice in the IND-CPA game hop. Second, the advantage in game 8 is bounded by zero as the secrecy of bit b in game 8 is trivial as explained before.
These advantages are put together to form the final result advantage.

The advantage depends on some parameters like the length of the plaintexts and the time. CryptoVerif also defines the result time as the time of the relevant operations used.

TeX output

CryptoVerif also allows writing its output to a TeX file. You can see an example in the following.

mkdir tex
./cryptoverif -tex ./tex/enc-then-MAC-IND-CPA examples/basic/enc-then-MAC-IND-CPA.ocv

You can view the PDF with a TeX editor of your choice (e.g. TeXstudio).
Alternatively, you can simply use an Online LaTeX Editor to display the PDF without any installation required.